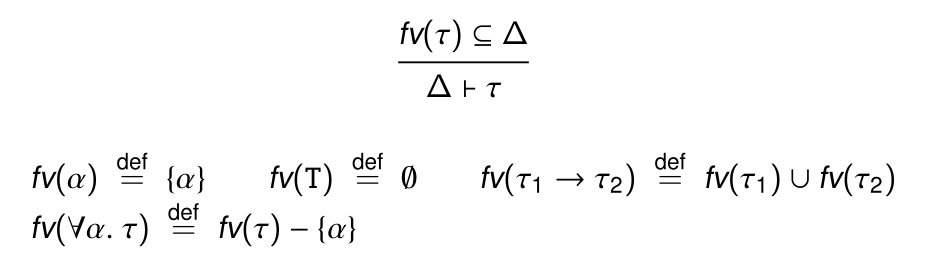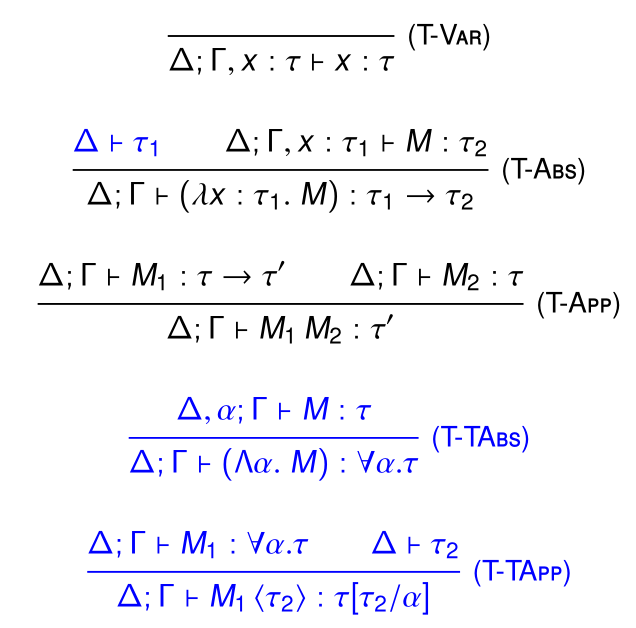本章是对STLC的进一步扩展。上图:
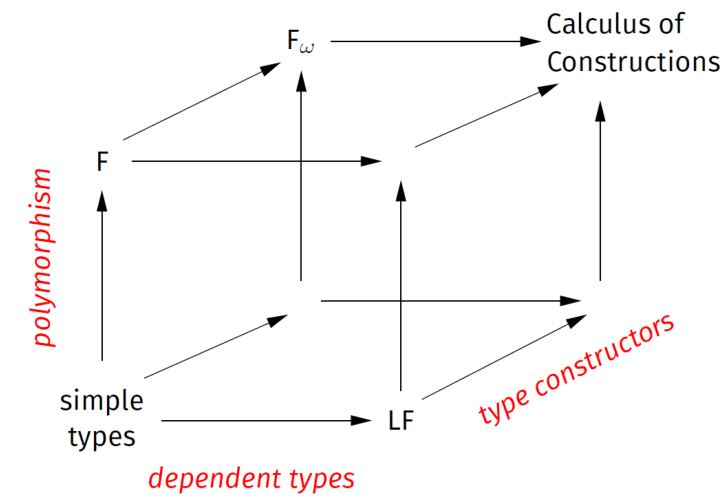
STLC还可以通过三个维度进一步扩展:多态性、构造性和依赖类型。本章将涉及多态(System F)和构造性(System Fω)。
Polymorphism(System F)
我们在λ-Calculus里会遇到这样一种场景:很多函数的函数体是相同的,但参数的类型不同。System F便对参数进行“多态”,而对函数体本身保持不变。这和编程语言,如Java的多态是不一样的,这些语言可以通过不同的类型指定不同的行为。
Syntax
(Types)(Terms)(Values):τ::=α ∣ T ∣ τ→τ ∣∀α.τ:M::=x ∣ λx:τ. M ∣ M M ∣ ∣ ∧α.M ∣ M⟨τ⟩:v::=λx:τ. M ∣ ∧α.M
(Contexts)(TypeVarContexts):Γ::=⋅ ∣ Γ, x:τ:Δ::=⋅ ∣ Δ, α
Reduction

Δ对每一种Type的formulation:
Δ,α⊢α
Δ⊢T
Δ⊢τ1→τ2Δ⊢τ1Δ⊢τ2
Δ⊢∀α.τΔ,α⊢τ
或者用Free variavle的方式定义:
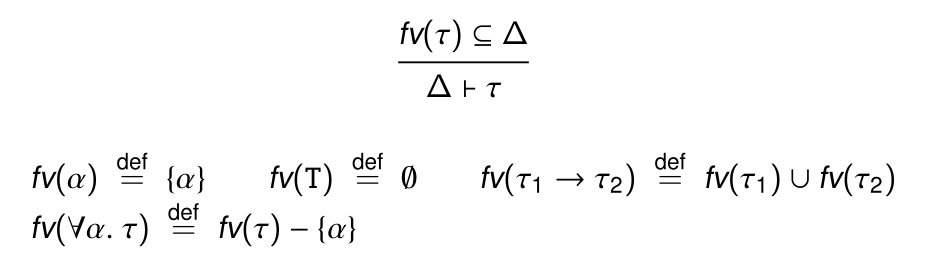
Typing
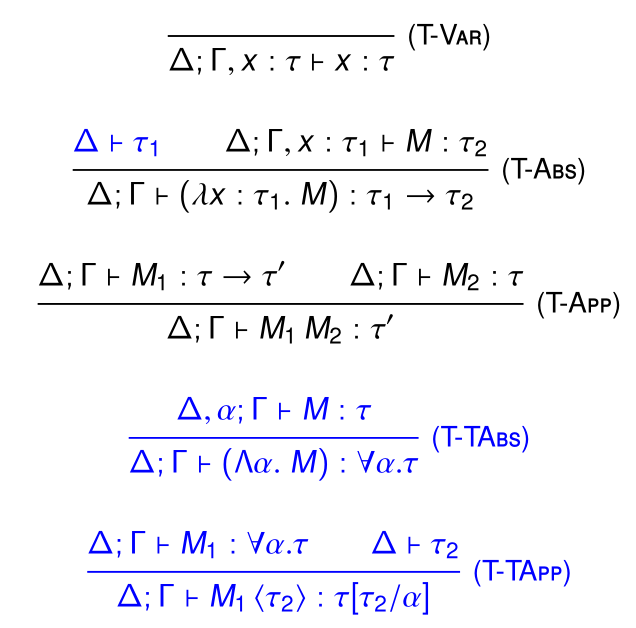
举个例子:

可以看到Rule的应用还是很简单的,除了相较STLC可以定义诸如(\lambda x. x x)等Term,因为其中的x可以通过多态来区分对待/
Properties
之前的STLC的Preservation和Progress仍然保留,并且增加了Strong normalization:每一个well-typed System F Term,无论通过何种reduction path,最终都会终止Reduction。
Church Encodings
我们可以通过System F来Encode之前Untyped λ-calculus通过Church Encoding定义的values。例如,可以将布尔值定义为:
TrueFalsenot=∧α.λx:α. λy:α.x=∧α.λx:α. λy:α.y=λb:Bool. ∧α.λx:α.λy:α. b⟨α⟩ y x
其中,Bool的类型为∀α→α→α,not类型为Bool→Bool。
相对应的,我们还可以定义Church numerals:

Incompleteness?
在STLC里,我们会拒绝那些可能会出错的Term,如:
(λx.(x(λy.y))(x3))(λz.z)
在System F中,这是可以正常赋Type的:
λx:∀α.α→α.(x⟨Nat→Nat⟩(λy:Nat.y))(x⟨Nat⟩3)(∧α.λz:α.z)
当然,诸如(λx.x x)(λx.x x)的不可终止的Term仍然无法在System F定义。
Parametricity
System F对参数进行多态,但在实际过程中,我们如果只知道多态化的参数,推导出来Term的类型,是很难知道这个Term具体行为的。
比如,很多函数的类型都可以是∀α.α→α,他们的行为都可以划归成恒等函数∧α.λx:α.x.
然而,如果类型为∀α.α→α→α,只有两种类型即,前文提到的True和False。
因此,这部分实际上和自由度理论有关,这部分就是扩展内容了。
Constructive(System Fω)
Type层面的抽象和应用能让我们写出毫无意义的Type Expresssion,比如Type层面的(Bool Nat)和Term层面的(True 6)一样是毫无意义的。
因此,本章在Type的上层再扩展Kind,从而对Type expression进一步进行归类。
(Kinds):κ::=∗ ∣ κ→κ
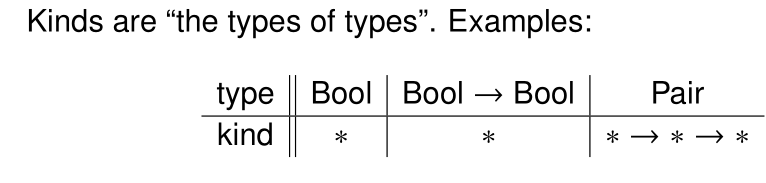

既然我们又加了一层Kind,还能给Kind再进行抽象,继续扩展吗?
当然可以,但三层已经足够我们对现有的静态类型语言进行抽象。实际上,现有的如Java的语言并没有提供过多的类型操作符。
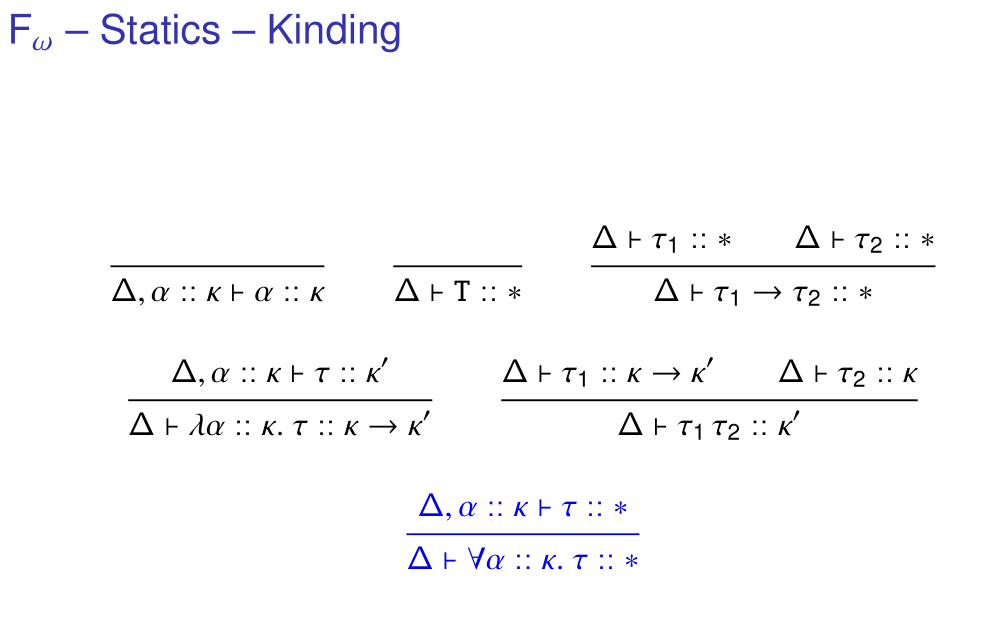
Statics
System Fω对已有的Terms/Kinds/Types/Values进一步修改:
λω

而对Kind的Kinding/Typing Rules等等,在这里就单纯截图了(因为确实不是重点,我也看不懂)
实际上就是我懒了😤
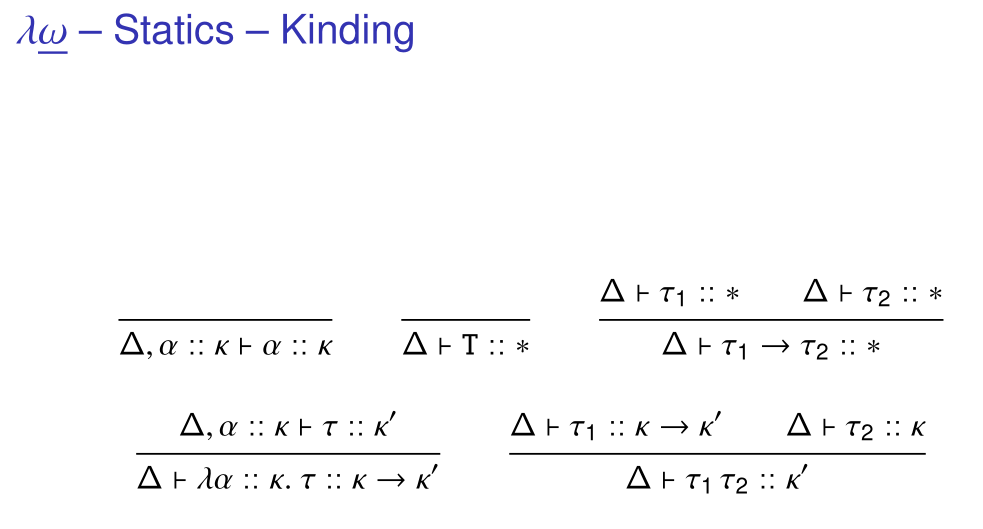


Fω